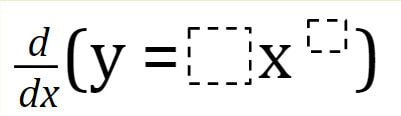Calculus 12 Derivatives
Specific Curriculum Outcomes
A2 Demonstrate an understanding of the definition of the derivative.
C4 Demonstrate an understanding of the connection between the graphs of f and f’.
B5 Find where a function is not differentiable and distinguish between corners, cusps, discontinuities, and vertical tangents.
B6 Derive, apply, and explain power, sum, difference, product and quotient rules.
B7 Apply the chain rule to composite functions
B8 Use derivatives to analysis and solve problems involving rates of change.
B9 Apply the rules for differentiating the six trigonometric functions
A3 Demonstrate understanding of implicit differentiation and identify situations that require implicit differentiation
B10 Apply the rules for differentiating the six inverse trigonometry functions (optional)
B11 Calculate and apply derivatives of exponential and logarithmic functions
B12 Apply Newton’s method to approximate zeros of a function (optional)
B13 Estimate the change in a function using differentials and apply them to real world situations
B14 Solve and interpret related rate problems
A2 Demonstrate an understanding of the definition of the derivative.
C4 Demonstrate an understanding of the connection between the graphs of f and f’.
B5 Find where a function is not differentiable and distinguish between corners, cusps, discontinuities, and vertical tangents.
B6 Derive, apply, and explain power, sum, difference, product and quotient rules.
B7 Apply the chain rule to composite functions
B8 Use derivatives to analysis and solve problems involving rates of change.
B9 Apply the rules for differentiating the six trigonometric functions
A3 Demonstrate understanding of implicit differentiation and identify situations that require implicit differentiation
B10 Apply the rules for differentiating the six inverse trigonometry functions (optional)
B11 Calculate and apply derivatives of exponential and logarithmic functions
B12 Apply Newton’s method to approximate zeros of a function (optional)
B13 Estimate the change in a function using differentials and apply them to real world situations
B14 Solve and interpret related rate problems
activities
- Introducing Calculus Activities from Underground Mathematics - A number of rich tasks for introducing calculus concepts design at the University of Cambridge.
- How Steep is this Hill? Desmos Activity from David Petro - This activity is meant to be an introductory activity for Calculus. It tries to draw out several ideas. 1) that if you zoom into any curve enough it can be approximated by a straight line, 2) to approximate the slope of a curve we can use a straight line and 3) to calculate the slope of that line at any point, we should choose two points on the curve that are very close to each other. Ideally, I envision giving this to students as a homework piece to warm them up for the main lesson on slopes of secants and tangents.
- Sketchy Derivatives Desmos Activity from Desmos - In this activity, students respond to a variety of graph-sketching prompts to demonstrate (and deepen) their understanding of the graphs of derivatives. This activity is designed for students with at least some experience in sketching derivatives.
|
- Why is it Called the Chain Rule? video from Tipping Point Math - A description of the chain rule using visuals relating to gear ratios.
- Derivative Matching Cards from David Petro - Students are give a set of cards with the graph of either a linear, quadratic or cubic function on them. Their job is to pair up the graphs of the functions with the graphs of the derivatives. There are a total of 12 functions with 12 derivatives. There is a Desmos Card Sort Activity that was inspired by this activity.
|
- Implicit Differentiation Sorting Activity from Caitlyn Gironda - Students sort cards showing the steps of several implicit differentiation problems.
- Related Rates, Yet Another Redux from Sam Shah - Sam has some great ideas on introducing related rates. He has a very nice worksheet (Dan Meyer even commented on it). I really like his idea of using balloons. He started class asking for a volunteer to blow up balloons. He taped an empty balloon, a balloon with one breath, with two breaths, etc to the whiteboard. Then the class had a discussion about what they could measure about the balloons and what changed with each balloon. This five minute start to class reinforced the main idea (hopefully). We changed one thing. It changed a bunch of other things. But just because one thing changed in one particular way doesn’t mean that everything changed in that same way. For example, just because the volume increased at a constant rate doesn’t mean the radius changed at a constant rate.
- Which One Doesnt Belong (WODB) Problems - You can use the problems to discuss continuity and differentiability.
- A fun way to Estimate the value of e from Mike Lawlor - Generate 64 random integers from 1 to 64 and put snap cubes on the squares of the chessboard to represent those numbers. How many of the squares end up with no cube on them? The ratio of 64 to empty squares is approximately e.