Mathematics 9 Square Roots and surface area
Specific Curriculum Outcomes
N05 Students will be expected to determine the exact square root of positive rational numbers.
N06 Students will be expected to determine an approximate square root of positive rational numbers.
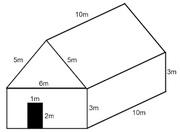
G01 Students will be expected to determine the surface area of composite 3-D objects to solve problems (note that this outcome is limited to right cylinders, right rectangular prisms, and right triangular prisms).
N05 Students will be expected to determine the exact square root of positive rational numbers.
N06 Students will be expected to determine an approximate square root of positive rational numbers.
G01 Students will be expected to determine the surface area of composite 3-D objects to solve problems (note that this outcome is limited to right cylinders, right rectangular prisms, and right triangular prisms).
N05 and N06 activities
- Quizizz Game from Erick Lee - An online formative assessment for square roots of perfect square rational numbers (N05). These 10 questions are similar to those found in the textbook.
- Placing a Square Root on the Number Line from Illustrative Mathematics - Ask students to place sqrt(28) on a number line accurate to 1 decimal place. You could repeat this activity with additional values or assign students to small groups and have each group place a given value on a common number line.
- Square Roots Clothesline Activity - Use a variety of visuals and benchmarks to locate perfect squares and approximate the value of non-perfect square numbers. A pdf file of cards already constructed for this activity from Andrew Stadel.
G01 Activities
|
- File Cabinet from Andrew Stadel - Andrew was staring at this file cabinet at the back of his room, saw a stack of Post-Its on his desk and thought, how many Post-Its would it take to cover this rectangular son-of-a-prism... and so it began. Extension: ask students to calculate how many post-it note it would take to completely cover their desk. Give them exactly that many post-its and see if it works.
|
|
- Surface Area Tin Man Project - Each pair of students built a tin man out of boxes, toilet paper rolls, paper towel rolls, Styrofoam balls, and cones. They had to use a formula sheet to first measure the surface area of the parts, showing all of their work for each part. Next they had to tape the parts together. Then I would give them the exact amount of foil they measured for, no more and no less. They had to cover their tin man as completely as possible without running out of tinfoil or having extra leftover.