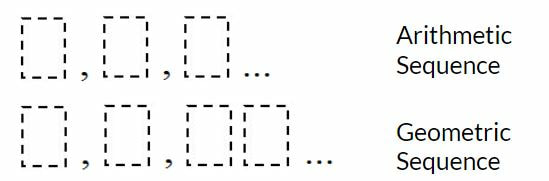Pre-Calculus 11 Sequences and Series
Specific Curriculum Outcomes
RF09 Students will be expected to analyze arithmetic sequences and series to solve problems.
RF10 Students will be expected to analyze geometric sequences and series to solve problems.
RF09 Students will be expected to analyze arithmetic sequences and series to solve problems.
RF10 Students will be expected to analyze geometric sequences and series to solve problems.
RF09 Activities (Arithmetic Sequences and Series)
|
| ||||||
- Linear Sequences from Ms. Konstantine - A collection of questions about arithmetic sequences.
- Plotting an Arithmetic Sequence using Desmos - A Desmos graph showing how to use a list, sliders and the formula for an arithmetic sequence to plot points.
- Magic and Arithmetic Series from Ted Lewis - A nice class opener to get students curious about a formula for finding the sum of an arithmetic sequence and learning about arithmetic series.
RF10 Activities (geometric sequences and series)
- Doodling to Infinity video on YouTube from Vi Hart - Vi Hart talks about infinite sequences in an artistic way.
- Getting Coins from the Bank from Carlos Sarraute/Alex Bellos - Alex poses a coin problem. "It takes place on a grid with an infinite number of rows and columns, and it starts with three coins in the top left corner of the grid." "The game has one move. At any moment you can remove any coin, and replace it with two coins, one in the cell immediately below the removed coin, and one in the cell immediately to the right of the removed coin. There’s one more thing. You are only allowed to remove a coin, in the way described above, if the cell below that coin and the cell to the right of that coin are empty. In other words, if a coin has an empty cell below it and an empty cell to its right, then you can remove that coin and replace it with two coins, one immediately below and one immediately to the right of the cell of the removed coin." The square of four cells in the upper left corner are called the 'bank." That’s it. There are no more rules. Let’s redraw the initial grid with a red line separating the four cells in the upper left corner. These four cells are called the ‘bank’. The challenge is to try to remove all of the coins from the bank or prove that it is impossible. There is a great solution to this problem using infinite series.
|
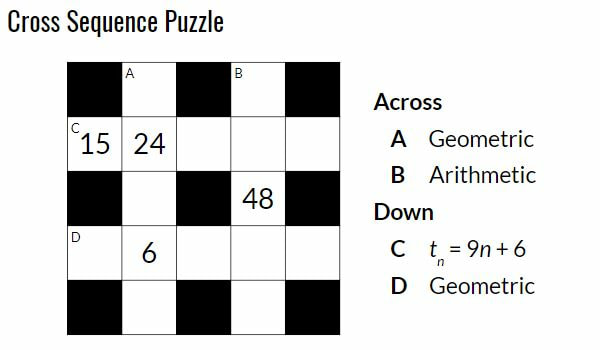
- Cross Number Puzzles - Create a puzzle for your student to solve and then ask them to make their own. Inspired by https://www.mathspad.co.uk/i2/teach.php?id=crossSequences3
|
| ||||||
- Geometric Series Formula YouTube video from James Tanton - What is the geometric series formula? When is it valid? How do we derive the formula? All explained by James Tanton, the Mathematician in Residence at the Mathematical Association of America in Washington D.C.
- The Paper Master Activity from Sam Shah - An excellent introduction to infinite geometric series using a single sheet of paper and groups of three students. A similar activity is found in our textbook, problem #23 (mini-lab) on p65.
- Super Ball from Dan Anderson - Use a bouncing super ball to model an infinite geometric sequence. Each time the ball bounces, it has 92% of its previous height.