mathematics 7 data analysis
Specific Curriculum Outcomes
SP01 Students will be expected to demonstrate an understanding of central tendency and range by
SP02 Students will be expected to determine the effect on the mean, median, and mode when an outlier is included in a data set.
SP04 Students will be expected to express probabilities as ratios, fractions, and percents.
SP05 Students will be expected to identify the sample space (where the combined sample space has 36 or fewer elements) for a probability experiment involving two independent events.
SP06 Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events.
SP01 Students will be expected to demonstrate an understanding of central tendency and range by
- determining the measures of central tendency (mean, median, mode) and range
- determining the most appropriate measures of central tendency to report findings.
SP02 Students will be expected to determine the effect on the mean, median, and mode when an outlier is included in a data set.
SP04 Students will be expected to express probabilities as ratios, fractions, and percents.
SP05 Students will be expected to identify the sample space (where the combined sample space has 36 or fewer elements) for a probability experiment involving two independent events.
SP06 Students will be expected to conduct a probability experiment to compare the theoretical probability (determined using a tree diagram, table, or other graphic organizer) and experimental probability of two independent events.
SP01 and SP02 activities
|
- Mean, Median, Mode and Range with Linking Cubes - Ask each student to reach into a large box of linking cubes to grab as many as they can with one hand. Students then build a tower with their linking cubes. As a class, student to line up their towers in order from shortest to tallest. To get the class range, subtract the height of the shortest tower from the tallest tower. Is there a height that occurs more often than any other? That is the mode. To get the median, find the tower in the middle of the row (if an even amount of towers, average the two middle towers). To get the mean, even out all the towers until they are the same height saving any "left over". Suppose you had 12 towers, each with a height of 10 and 5 remainder cubes. This would give a mean of 10 and 5/12 cubes.
|
- Paper Airplanes for Measures of Central Tendencies from Julie Reulbach - Students create paper airplanes and fly them to collect data and record it with a Google Form. They then use this data to calculate a variety of measures and create several different types of graphs.
- Mean Paper Airplanes from Bruno Reddy - Mr. Reddy uses a paper airplane contest to necessitate the need for calculating an average. To win fairly you probably need to throw more than once to account for variances in skill, luck and craftsmanship. In throwing more than once you introduce a dilemma – how do you choose a winner?
|
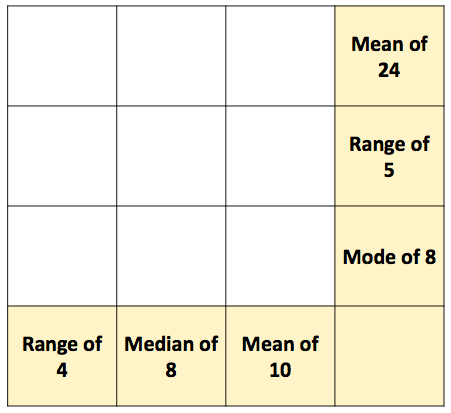
- Mean, Median, Mode, and Range Spider Puzzles from Sarah Carter - Sarah uses several spider puzzles involving mean, median, mode and range. These puzzles should bring about plenty of discussion. Four "spiders" of increasing difficulty asking students to complete a list of numbers to make the average and range properties true.
|
|
SP04, SP05 and SP06 Activities
- The Two-Dice Sum Game from Marilyn Burns as explained by Joe Schwartz - Each student makes a number line from 2 to 12. Students get to place 11 counters on this number line. Roll two dice and if there is a counter on that number, remove it. The first student to remove all their counters from their number line wins. Can students find the best way to allocate their counters?
- Dibingo from Don Steward - In this game, students have to pick a card with different values on it. Students take turns rolling two dice. If there sum is a number that is on their card, they score a point. Which card will give you the best chance of winning? Megan Schmidt wrote about using this game in her classroom.
- Card Game from Mathematical Assessment Project - Students use probability to make predictions about a card game. Ten cards, numbered 1 to 10, are shuffled and placed face down so that the numbers do not show. The cards are turned over one at a time. The class has to find the probability that the next card will have a higher number than the last one turned.
|
| ||||||