Mathematics 8 Measuring Prisms and cylinders
Specific Curriculum Outcomes
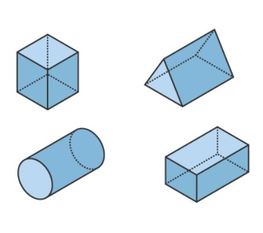
M02 Students will be expected to draw and construct nets for 3-D objects.
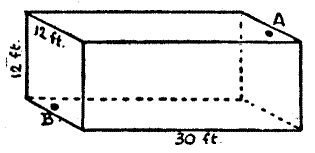
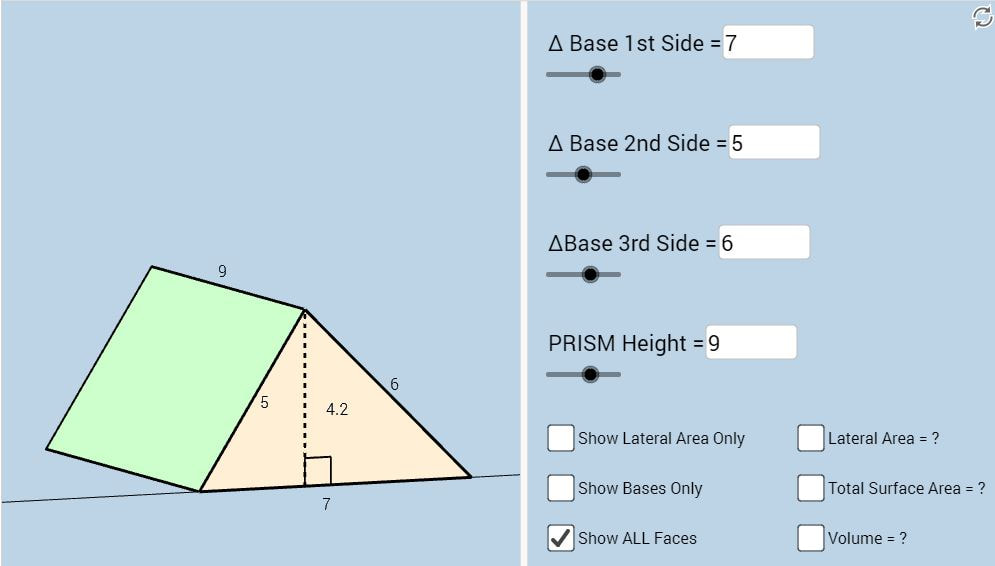
M03 Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems.
M04 Students will be expected to develop and apply formulas for determining the volume of right rectangular prisms, right triangular prisms, and right cylinders.
M02 Students will be expected to draw and construct nets for 3-D objects.
M03 Students will be expected to determine the surface area of right rectangular prisms, right triangular prisms, and right cylinders to solve problems.
M04 Students will be expected to develop and apply formulas for determining the volume of right rectangular prisms, right triangular prisms, and right cylinders.
M02 activities
|
|
- Tetrahedron Wall Art - Students create a mural by cutting and folding nets of right pyramids made from different coloured paper.
|
M03 and M04 Activities
- Area Maze Puzzles by Naoki Inaba - A nice class warm-up logic puzzle to get students thinking about area.
|
- File Cabinet from Andrew Stadel - How many post-it notes will it take to cover Mr. Stadel's file cabinet? Students calculate a solution and then see if it matches the actual solution... or if you have a lot of sticky notes lying about, you can cover your own file cabinet.
- Surface Area of a Multi-link Cube Prism - Have students construct a 1x2x3 rectangular prism with multi-link cubes. Then challenge them to add cubes on to this prism to double the surface area.
- Surface Area & Volume Scavenger Hunts from @g_brgmn - Greta describes a "loop" activity to review surface area and volume. On the top of a sheet of paper she puts the first problem. Then she puts the answer to that problem on the bottom of the next sheet. Then on the top of that sheet she puts the next problem. The final answer goes on the bottom of the first sheet. Students can start at any card. They solve the problem and find that answer on another sheet. This continues until they have done all the problems. If they do everything correctly, they will end up back where they started.
|
- [3 Act Lesson] Sandboxes: Volume of Cylinders (& Spheres) from Jonathan Newman - Jonathan is building a sandbox. How much more expensive will the sand be for an 8' x 8' box than a 6' x 6' box? What about a 6' or 8' diameter circular sandbox?
- Hands-on Surface Area Activity from Erick Lee - Students work in pairs to create a net of a rectangular or triangular prism on a piece of coverstock. They measure all of the edges and calculate the surface area of each face and the total surface area on the net. Then they cut out the net and tape it together.
|
- Would Your Rather... Pools from John Stevens - Would you rather have a pool with dimensions of 40 ft x 9 ft x 4 ft OR 7 yds x 4 yds x 2 yds? Whichever option you choose, justify your reasoning with mathematics.
- Multi-link Cube Prisms - Students in groups can explore how many different rectangular prisms they can build using a set amount of multi-link cubes. They can record volume and surface area for each rectangular prism they construct.
- Which One Doesn't Belong? from wodb.ca and Illustrative Math - Find a reason why each shape does not belong with the rest of the group. A great strategy for promoting classroom discussion.
- Popcorn Box - Create open-topped boxes from a sheet of centimetre grid paper by cutting away squares from the four corners and folding the sides up. Experiment to determine the dimensions of a box with the greatest volume given the same size grid paper. Do flat, wide boxes or tall narrow boxes have more volume?
|