Mathematics 8 Square Roots and Pythagorean Theorem
Specific Curriculum Outcomes
N01 Students will be expected to demonstrate an understanding of perfect squares and square roots, concretely, pictorially, and symbolically (limited to whole numbers).
N02 Students will be expected to determine the approximate square root of numbers that are not perfect squares (limited to whole numbers).
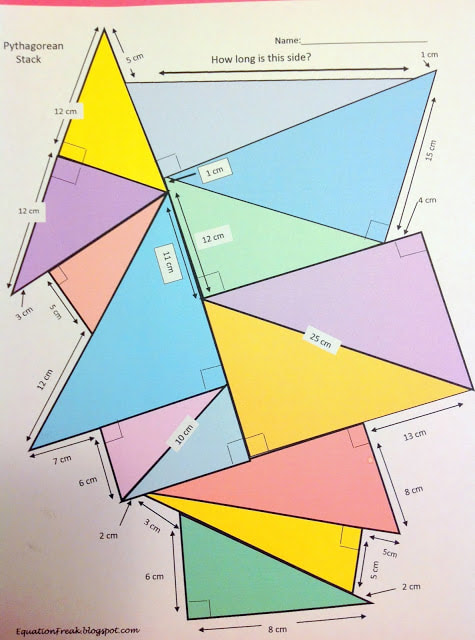
M01 Students will be expected to develop and apply the Pythagorean theorem to solve problems.
N01 Students will be expected to demonstrate an understanding of perfect squares and square roots, concretely, pictorially, and symbolically (limited to whole numbers).
N02 Students will be expected to determine the approximate square root of numbers that are not perfect squares (limited to whole numbers).
M01 Students will be expected to develop and apply the Pythagorean theorem to solve problems.
N01 and N02 activities
- The Locker Problem from Illustrative Mathematics - A nice review of perfect squares and factors would be the locker problem.
- Perfect Squares Puzzle from Sarah Carter and Resilience Leads the Way from Megan Schmidt - Place the numbers 1-15 (or 1-17) in a row such that adjacent pairs of numbers always sum to a perfect square. This is a fun puzzle to help students review perfect square numbers.
- Rational and Irrational Numbers from Open Middle - Using only numbers 1-8 (without repeating any number), create a rational number from a square root, an irrational number from a square root, an integer from a rational, a repeating decimal from a rational and a terminating decimal from a rational:
|
M01 Activities
- Pythagorean Theorem Water Demo video - A video demonstrating the Pythagorean Theorem using water.
- Tilted Squares from NRICH - This problem offers an opportunity to spot patterns, make generalizations and eventually discover Pythagoras's Theorem, while giving students the chance to practice working out areas of squares and right-angled triangles.
- Finding the Shortest Route: A Schoolyard Problem from the Mathematics Assessment Project - Students work together to try to find the shortest path around a school playground, touching each side of the playground and returning to where they started.
- Corner to Corner 3 Act Task from Jon Orr - Ask students to estimate the distance from one corner of a classroom to the opposite diagonal corner. Then ask students to calculate the distance. What information do they need to solve this problem?
|
- Pythagorean Theorem from Open Middle - What could the lengths of the legs of a right triangle be such that the lengths of the legs are integers and the hypotenuse is an irrational number between 5 and 7?
- Pythagorean Theorem with Starburst video - You could do this with any square candy or cracker.
- Squares, Area & The Pythagorean Theorem - Lisa started class by providing each student with a grid whiteboard and marker and asked them if they could draw a square whose area is 1 square unit. They did this with no problem and sat looking at me like I was crazy. Next, she asked if it was possible to draw a square whose area was 2 square units, with the corners on the grid. This was a bit harder. Then she asked students to try drawing a square with integer each area from 1-10 & students were engaged all period. She kept track of the areas that students thought were not possible.
- Watson Save from Yummy Math and Running on the Football Field from Illustrative Mathematics - In the 2005 AFC divisional football championship game between the New England Patriots and the Denver Broncos, Benjamin Watson stopped a touchdown in the last instant. He did this by running diagonally across the entire football field. Watch the video to see the play and listen to the commentary.
- Ladder Safety - Look at some images of unsafe ladder usage (a quick internet search will find some scary examples: just google "unsafe ladder pictures"). You could have students rank them from most safe to least safe. Have students brainstorm the elements of safe ladder usage. Focus on the slope that the ladder makes with the wall. For a certain sized ladder, how high up is it safe to go? You could use a ruler to make a scale model. If you know the height of the ladder and the distance from the wall, you could apply Pythagorean theorem and use square roots to calculate how far up a building a ladder can safely reach. (The angle of the ladder should be 1:4, that is 1 unit away from the supporting structure for every 4 units of height.)
- Applying the Pythagorean Theorem in a Mathematical Context from Illustrative Mathematics - Three right triangles surround a shaded triangle; together they form a rectangle measuring 12 units by 14 units.Is the shaded triangle a right triangle? Provide a proof for your answer.
- “When will I ever need Pythagoras?” - an honest response from Junaid Mubeen - "Pythagoras’ Theorem, then, is more than a formula: it exemplifies how mathematics is bound to logic, art and history. Three decent reasons to engage with those pesky triangles."