Mathematics 9 Similarity and Transformations
Specific Curriculum Outcomes
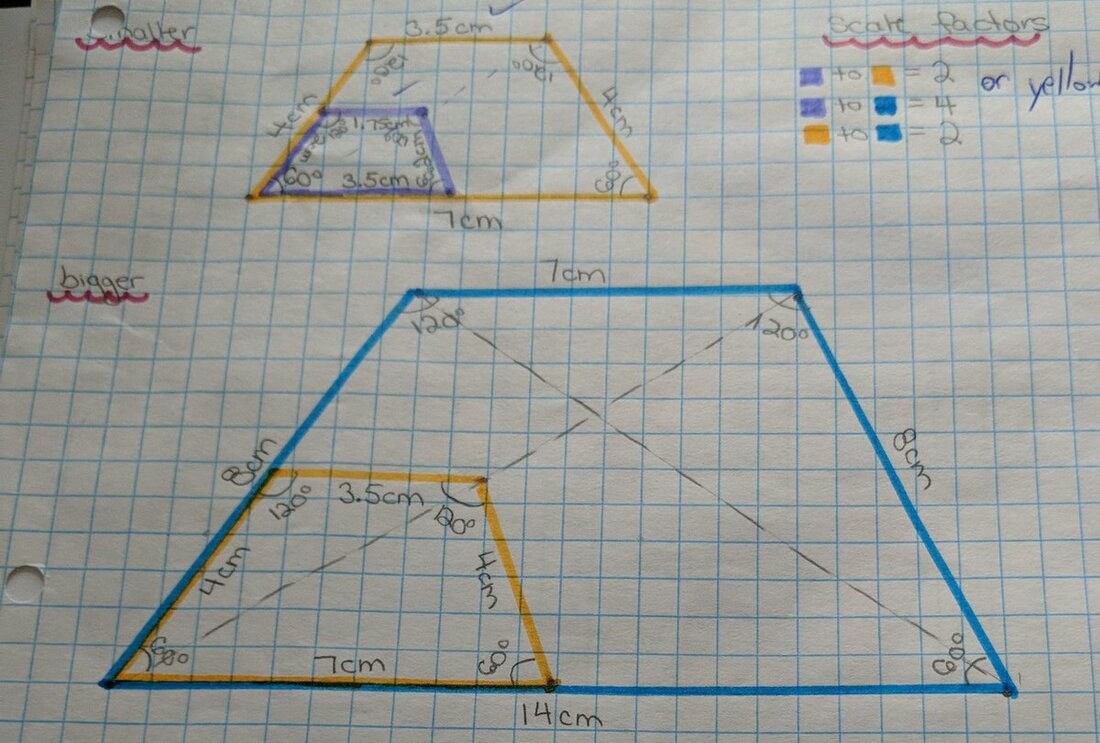
G03 Students will be expected to draw and interpret scale diagrams of 2-D shapes. *This outcome should be done in conjunction with outcome G02
G02 Students will be expected to demonstrate an understanding of similarity of polygons.
G04 Students will be expected to demonstrate an understanding of line and rotation symmetry.
G03 Students will be expected to draw and interpret scale diagrams of 2-D shapes. *This outcome should be done in conjunction with outcome G02
G02 Students will be expected to demonstrate an understanding of similarity of polygons.
G04 Students will be expected to demonstrate an understanding of line and rotation symmetry.
G03 activities
- Marcellus the Giant Desmos Activity in English and French - This activity will help your students understand the definition of a proportional relationship. They'll create a giant and then make sure all of his features are proportional. They'll see the representation of his proportions on a graph and manipulate the graph to see the giant change dynamically.
- Seven Lessons on Scaling - A variety of activities around scaling and ratio. There is a nice connection here to linear relations with pictures of patterns made with a ratio of pattern blocks.
- Exploring Scale Factor from Matt Coaty - Students select an image and glue to a 5 cm x 7 cm card and then draw a 1cm x 1cm grid on top of it. They then draw this image on a 15cm by 21cm grid (or some other proportional size) to make an enlarged image.
|
- Photographs Task from MAP Assessment Tasks - In this task, you need to figure out how to fit three different-sized photographs on a single sheet.
- The Incredible Shrinking Dollar from Dan Meyer - Dan shrinks a dollar bill on a photocopier. If Dan shrinks the dollar nine times like this, how big will it be? Will you still be able to see it?
- Big Cheques from Kyle Pearce - Kyle walks into the photocopy room, take a cheque out of his wallet and places it on the photocopier. He then begin to press the button to enlarge the photocopy repeatedly. What’s the question that comes to mind?
G02 Activities
- Water Slide Desmos Activity - Students will use equivalent ratios to create a smooth ramp for a water slide.
- Eye-to-Eye from Mr. Orr - Predict where a mirror should be placed on the ground between two people in order for them to be able to see eye-to-eye in the mirror. A great application of similar triangles.
- Measuring with Mirrors and Similar Triangles - Measuring the height of a flagpole or other tall object using a mirror and similar triangles. (similar to problem 13 on p351 in Chapter 7.4 of Math Makes Sense 9)
- Mini-Golf Similar Triangles from Fawn Nguyen - The challenge then was to get the ball into the hole. Since you can’t putt the ball directly into the hole due to the water hazard, you need to make a bank shot.
|
G04 Activities
- Flag Symmetry - Can you find a country or provincial flag with line and/or rotational symmetry? Design a flag for planet Earth that has line and/or rotational symmetry. Check out some suggestions for a Flag of the Earth. How about Oskar Pernefeldt's suggestion for The International Flag of Planet Earth.