Pre-calculus 12 Trigonometry
Specific Curriculum Outcomes
T01 Demonstrate an understanding of angles in standard position, expressed in degrees and radians.
T02 Develop and apply the equation of the unit circle.
T03 Solve problems, using the six trigonometric ratios for angles expressed in radians and degrees.
T04 Graph and analyze the trigonometric functions sine, cosine and tangent to solve problems.
T05 Solve, algebraically and graphically, first and second degree trigonometric equations with the domain expressed in degrees and radians.
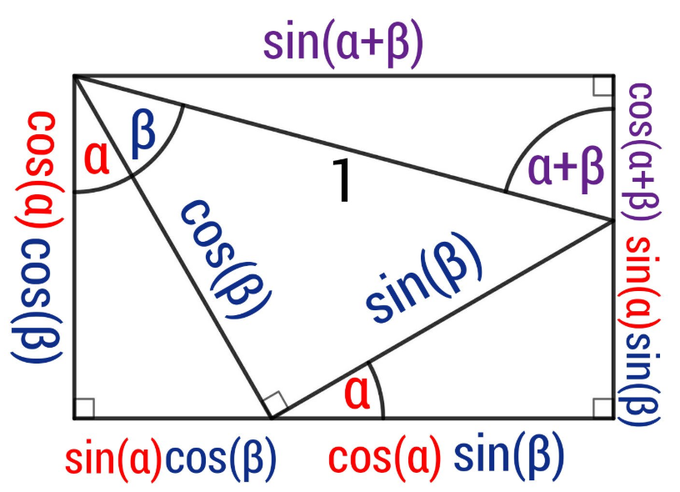
T06 Prove trigonometric identities, using: reciprocal identities, quotient identities, Pythagorean identities, sum or difference identities, and double-angle identities.
T01 Demonstrate an understanding of angles in standard position, expressed in degrees and radians.
T02 Develop and apply the equation of the unit circle.
T03 Solve problems, using the six trigonometric ratios for angles expressed in radians and degrees.
T04 Graph and analyze the trigonometric functions sine, cosine and tangent to solve problems.
T05 Solve, algebraically and graphically, first and second degree trigonometric equations with the domain expressed in degrees and radians.
T06 Prove trigonometric identities, using: reciprocal identities, quotient identities, Pythagorean identities, sum or difference identities, and double-angle identities.
T01 and T02 Activities
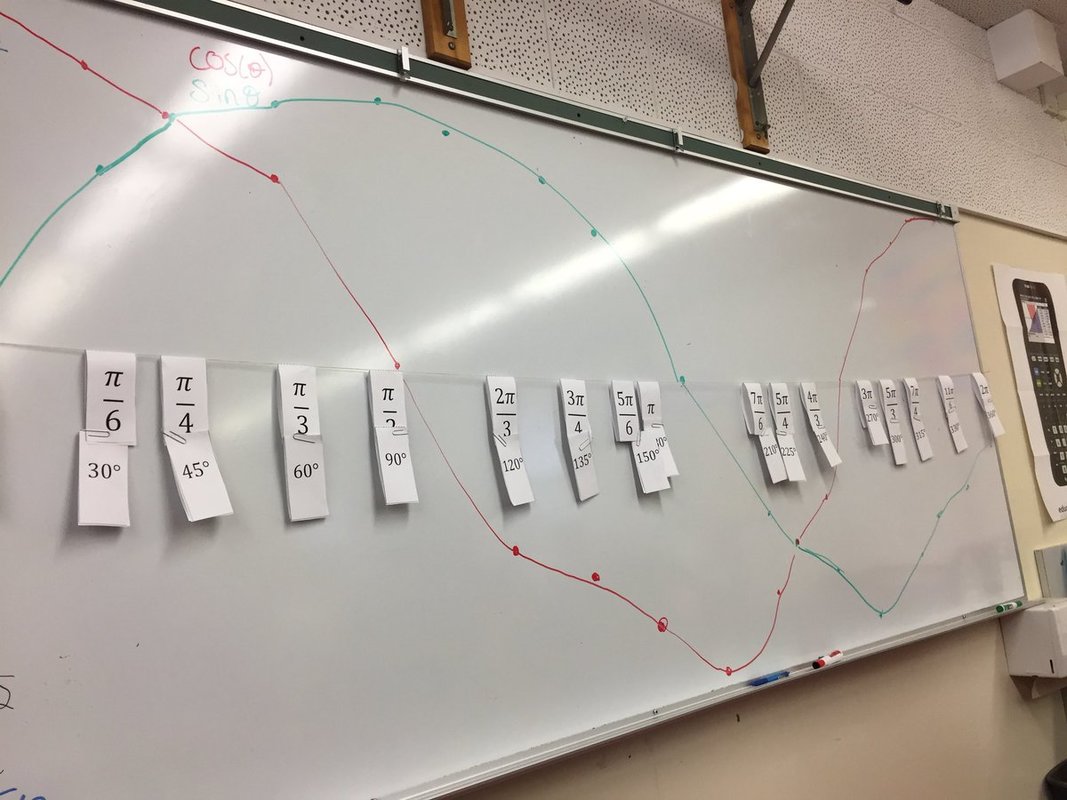
- A Prelude to Unit Circle Trigonometry from Sam Shah - Sam describes an activity to prepare students to understand the unit circle. Instead of starting with a circle, he primes students with thinking about x and y coordinates for other shapes. In this case he used a square, a rotated square and a triangle. Some very interesting graphs result.
T04 Activities
|
|
T05 Activities
|
T06 Activities
|
- Trig Identity Match Up Activity from Shireen Dadmehr - Students cut up a sheet containing statements from several trig identities. They then try to match up pairs of statements that are one step apart. They continue matching up statements until they have 4 complete trig identities.
- Math Market Trigonometry Review - Student buy questions from the market and sell solutions back for a profit. A fun activity to review of a variety of trig outcomes including solving equations and proving identities. A recording sheet for student work can be helpful.
- Inspiration is for Amateurs - I have often used this quote from Chuck Close when inspiring students to start trying things when solving trig identities. "The advice I like to give young artists [or mathematicians], or really anybody who’ll listen to me, is not to wait around for inspiration. Inspiration is for amateurs; the rest of us just show up and get to work. If you wait around for the clouds to part and a bolt of lightning to strike you in the brain, you are not going to make an awful lot of work. All the best ideas come out of the process; they come out of the work itself. Things occur to you. If you’re sitting around trying to dream up a great art idea, you can sit there a long time before anything happens. But if you just get to work, something will occur to you and something else will occur to you and something else that you reject will push you in another direction. Inspiration is absolutely unnecessary and somehow deceptive. You feel like you need this great idea before you can get down to work, and I find that’s almost never the case."